숫자야구
탄생 비화
숫자야구 져서 꼴받아서
처음에는 전체 숫자 풀에서 틀린 후보를 삭제해가는 식으로 했는데
Knuth 전략을 이용하면 6턴 내 클리어가 보장된다고 하여 공부할 겸 만들어 봄
구현 포인트
1. 피드백 클래스 생성
Knuth 전략의 핵심은 최악의 경우를 최소화하는 것이다.
각 추측마다 가능한 모든 피드백 그룹을 만들고, 가장 큰 그룹의 크기를 최소화한다.
피드백 그룹을 비교하기 위해 피드백 클래스를 생성해 관리한다.
// 피드백 결과를 구조화해서 비교하고 후보군을 나누기 위해 피드백 클래스 생성
private static class Feedback {
int strikes;
int balls;
public Feedback(int strikes, int balls) {
this.strikes = strikes;
this.balls = balls;
}
@Override
public boolean equals(Object object) {
if (this == object) return true;
if (!(object instanceof Feedback)) return false;
Feedback feedback = (Feedback) object;
return strikes == feedback.strikes && balls == feedback.balls;
}
@Override
public int hashCode() {
// Map에서 올바르게 비교되도록 해시코드 설정
return Objects.hash(strikes, balls);
}
}
2. 최적의 추측 선택
남은 후보군, 전체 후보군을 받아서 최악의 경우를 계산한다.
피드백 그룹의 크기를 최악의 경우로 판단해서 그 숫자가 가장 작은 것을 선택한다.
// 최적 추측 선택
private static String chooseBestGuess(List<String> candidates, List<String> allCandidates, Set<String> triedGuesses) {
int minWorst = Integer.MAX_VALUE;
String bestGuess = null;
// 모든 추측을 가지고 후보군과 비교해 가장 피드백이 많이 나오는 그룹 수를 계산한다(최악의 경우)
for (String guess : allCandidates) {
// 이미 시도한 추측은 건너뛰기
if (triedGuesses.contains(guess)) continue;
Map<Feedback, Integer> map = new HashMap<>();
for (String actual : candidates) {
Feedback f = getFeedback(actual, guess);
map.put(f, map.getOrDefault(f, 0) + 1);
}
// Knuth 전략의 핵심, 최악의 경우 계산 (가장 많은 후보가 남는 경우)
int worst = Collections.max(map.values());
// 더 나은 추측을 찾았거나, 동일한 최악의 경우에서 더 작은 숫자를 선택
if (worst < minWorst || (worst == minWorst && guess.compareTo(bestGuess) < 0)) {
minWorst = worst;
bestGuess = guess;
}
}
return bestGuess;
}
3. 입력 받아 판단 수행
추측에 대한 결과를 입력받아 다음 추측을 제시하는 부분.
최종적인 답이 나올때 까지 반복문을 돌린다.
while (true) {
// 1턴에서는 추측이 의미 없으므로 1234를 제시하고 결과를 받도록 한다.
String guess = "1234";
if (turn != 1) {
guess = chooseBestGuess(candidates, allCandidates, triedGuesses);
}
triedGuesses.add(guess); // 시도한 추측 기록
System.out.println(turn + "턴) 추천 추측: " + guess);
System.out.print("입력 (예: 1s2b / 3s / 2b / o): ");
// 추천 추측에 대한 결과를 입력받는다.
String input = sc.nextLine().trim().toLowerCase();
if (input == null || input.length() == 0) {
System.out.println("입력 없음");
continue;
}
int strikes = 0;
int balls = 0;
// 정규식으로 스트라이크 볼 패턴 구분
Pattern pattern = Pattern.compile("^(\\d+s)?(\\d+b)?$|^(\\d+b)?(\\d+s)?$");
if (input.equals("o")) {
// 아웃은 0s0b 따로 할 거 없음
strikes = 0;
balls = 0;
} else if (pattern.matcher(input).matches()) {
Matcher m = Pattern.compile("(\\d+)s|(\\d+)b").matcher(input);
while (m.find()) {
if (m.group(1) != null) {
strikes = Integer.parseInt(m.group(1));
}
if (m.group(2) != null) {
balls = Integer.parseInt(m.group(2));
}
}
} else {
System.out.println("잘못된 입력 형식");
continue;
}
Feedback feedback = new Feedback(strikes, balls);
List<String> filter = new ArrayList<>();
// 피드백을 입력받으면 정확히 일치하는 후보만 남김
for (String c : candidates) {
if (getFeedback(c, guess).equals(feedback)) {
filter.add(c);
}
}
// 필터가 비면 잘못된 것...
if (filter.isEmpty()) {
System.out.println("후보가 없습니다. 입력값을 확인해 주세요.");
continue;
}
// 후보군을 필터로 갱신
candidates = filter;
if (candidates.size() == 1) {
// 유일한 정답 출력 후 종료
System.out.println("정답: " + candidates.get(0));
break;
}
turn++;
}
완성
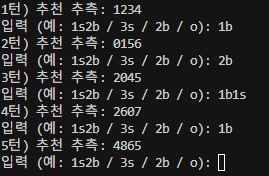
1차 테스트 숫자는 4865
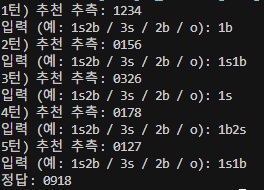
2차 테스트 숫자는 0918
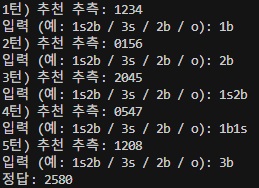
3차 테스트 숫자는 2580
반성
사실 이 상태에서는 아웃에 대한 판단이 잘못되어있다.
숫자 4개를 통으로 날릴 수 있는 아웃이 아무리 생각해도 최대 효율인데 왜 최악으로 판단되지?
Knuth 전략에서는 피드백 그룹의 크기로 최악의 그룹을 찾는다.
그런데 아웃의 경우 (0s0b) 그룹에 속하는 후보가 많을 수 있어서 최악의 경우로 판단된다.
- 인간) 4개 다 아니네? 개꿀 ㅋㅋㅋㅋ
- 깡통) 0s0b 그룹이 너무 많네? 이것은 최악의 경우이다.
최적화를 위해서는 단순히 그룹의 크기로만 판단하지 않고 정보량을 고려해야 한다.
아웃에 가중치를 주고 아웃을 우수한 추측으로 간주하도록 설정(점수제 도입)하면 더 나은 로직을 짤 수 있다.
하지만 현 상태로도 6턴 내 클리어가 보장되며, 감히 숫자야구 덤비는 애송이들의 뚝배기를 조각낼 수 있기 때문에 여기서 스탑.
코드 확인