던전 생성기 02
개요
남은 두개의 알고리즘으로 맵 만들기
즐 겁 다 !!
구현
1. Delaunay Triangulation + MST
얘는 왜 두개가 합쳐졌느냐???
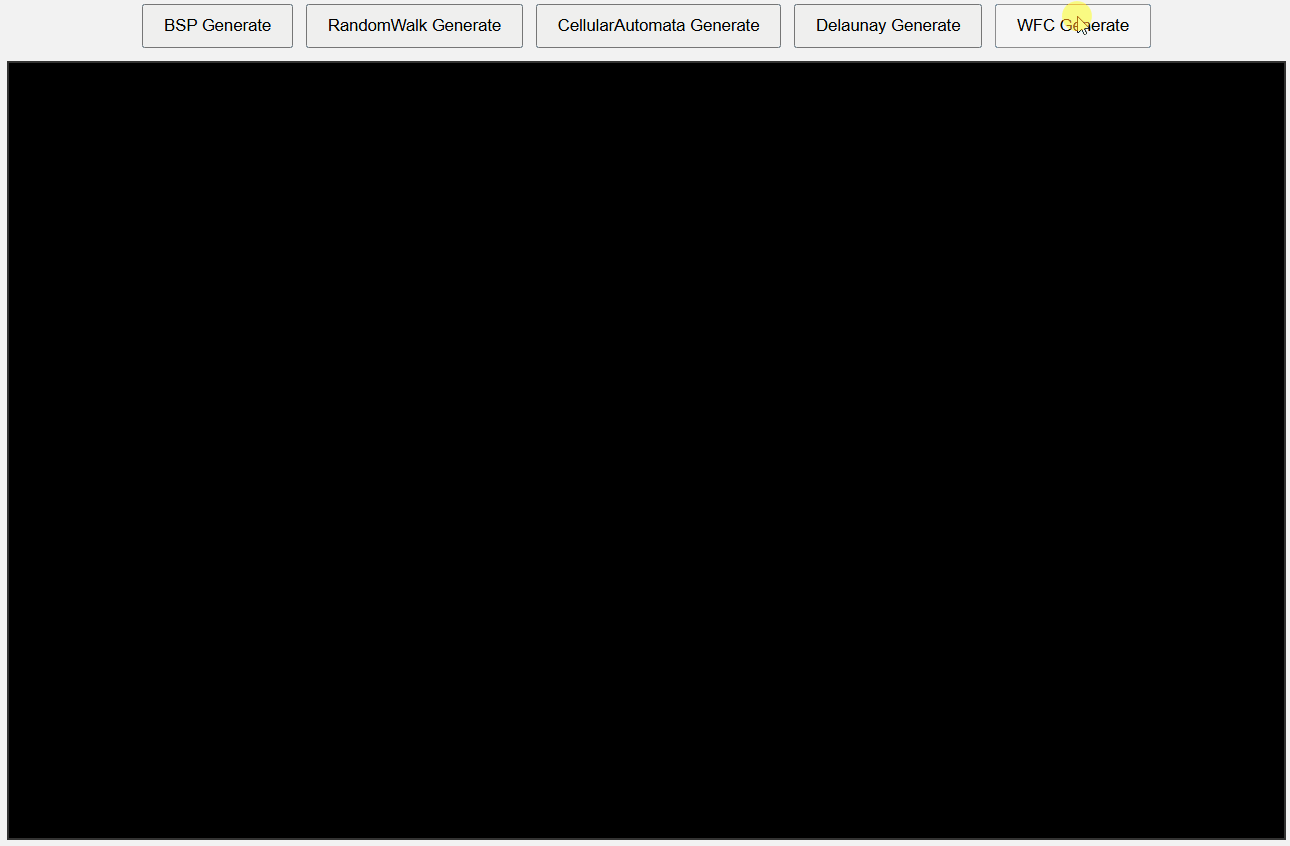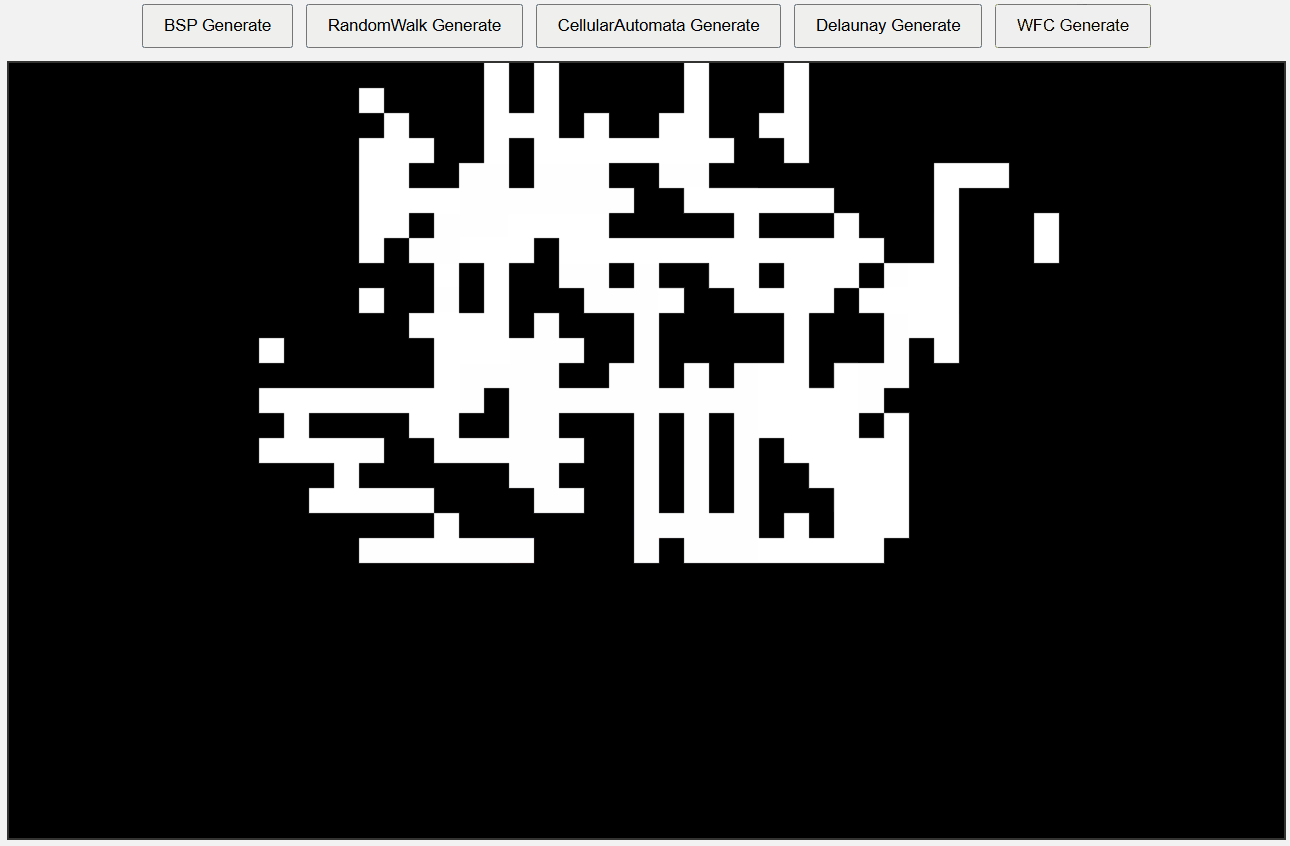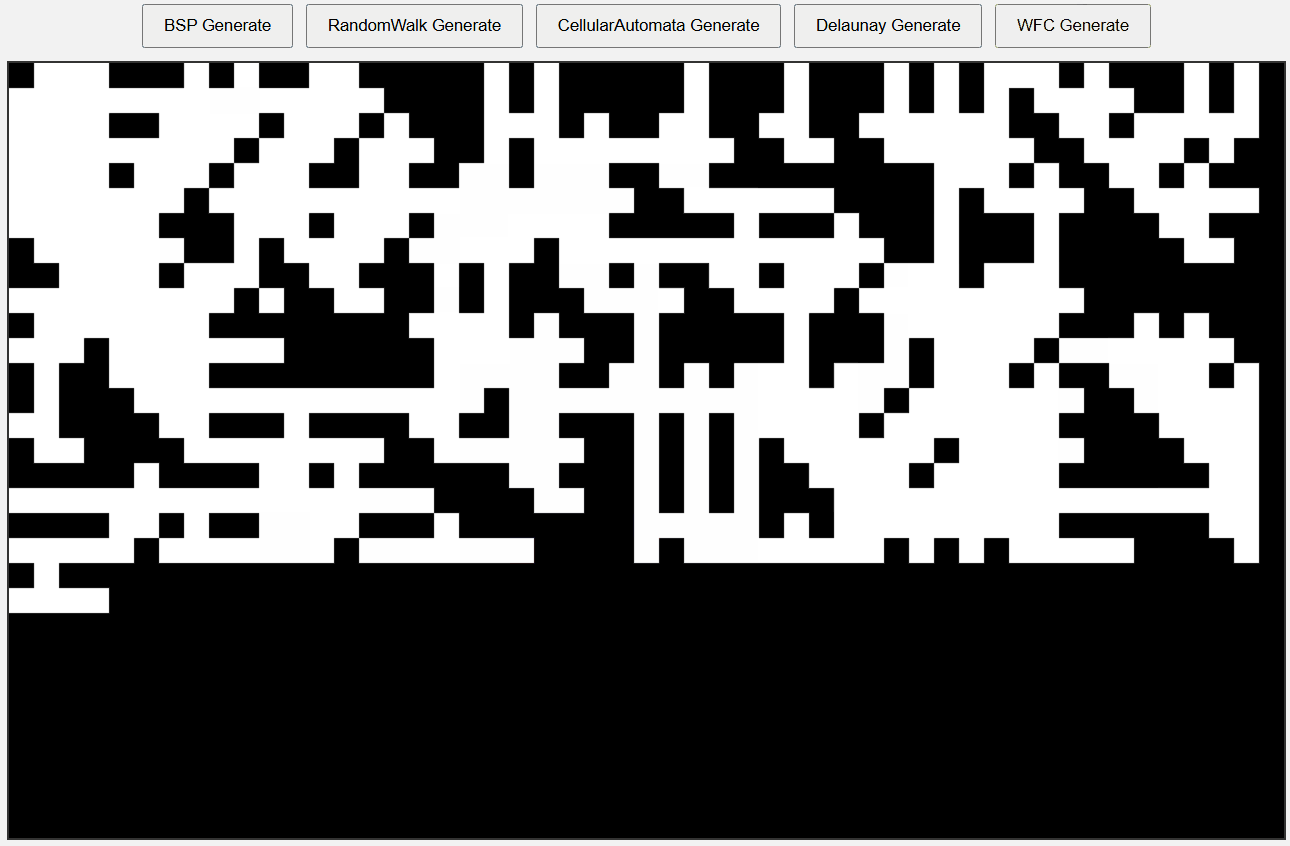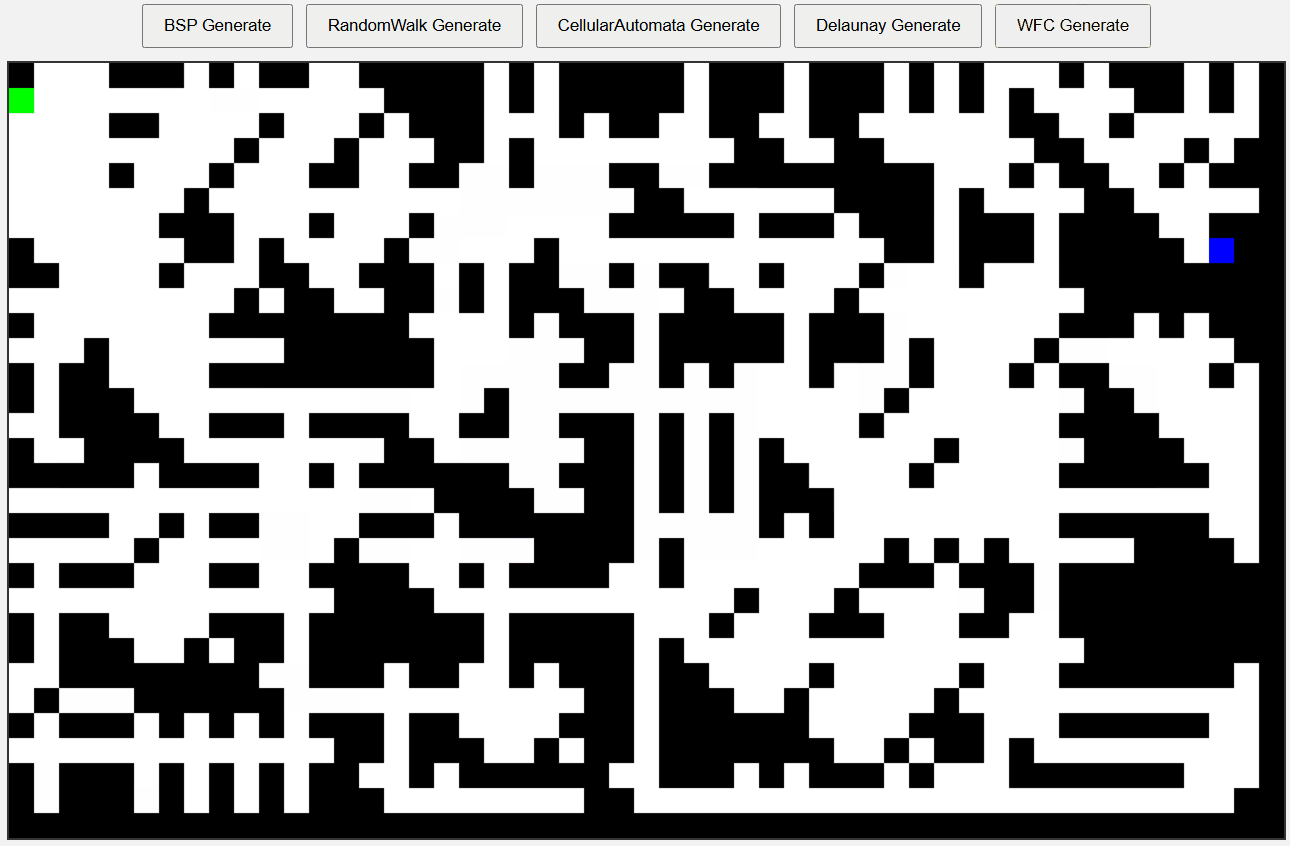
우선 랜덤한 점을 방의 중심점으로 사용해 방을 넒힌다.
그리고 Delaunay Triangulation 알고리즘으로 모든 점을 삼각형으로 연결해
각 삼각형의 외접원이 다른 점을 포함하지 않도록 최적의 삼각형 분할을 생성한다.
마지막으로 MST 알고리즘은 모든 방을 연결하는 최소 비용의 통로를 생성한다.
Delaunay Triangulation만 사용할 경우 모든 점이 서로 연결되어 너무 많은 통로가 생성되어 어지럽다.
이를 커버하는게 MST의 역할이다.
덕분에 자연스러운 방 배치와 효율적인 통로 연결이 이루어지게 된다.
삼각형 생성이 중요한데 삼각형을 생성하는 것으로 아래와 같은 일들이 가능해진다.
- 국지적 연결을 최적화해 가까운 방들끼리 통로가 생기는 기반 마련
- 삼각형의 변이 후보 연결선이 됨
- 삼각형은 면을 채울 수 있는 기본 단위라 공간을 균형있게 분할하기 유리함
이렇게 생성된 삼각형들을 MST가 간소화해 효율성을 확보한다.
// 점 클래스
class Point {
constructor(x, y) {
this.x = x;
this.y = y;
}
equals(other) {
return this.x === other.x && this.y === other.y;
}
}
// 간선 클래스
class Edge {
constructor(p1, p2) {
this.p1 = p1;
this.p2 = p2;
this.weight = Math.sqrt(
Math.pow(p2.x - p1.x, 2) + Math.pow(p2.y - p1.y, 2)
);
}
}
// 삼각형 클래스
class Triangle {
constructor(p1, p2, p3) {
this.p1 = p1;
this.p2 = p2;
this.p3 = p3;
}
// 외접원의 중심과 반지름 계산
circumcircle() {
const d = 2 * (this.p1.x * (this.p2.y - this.p3.y) +
this.p2.x * (this.p3.y - this.p1.y) +
this.p3.x * (this.p1.y - this.p2.y));
const ux = ((this.p1.x * this.p1.x + this.p1.y * this.p1.y) * (this.p2.y - this.p3.y) +
(this.p2.x * this.p2.x + this.p2.y * this.p2.y) * (this.p3.y - this.p1.y) +
(this.p3.x * this.p3.x + this.p3.y * this.p3.y) * (this.p1.y - this.p2.y)) / d;
const uy = ((this.p1.x * this.p1.x + this.p1.y * this.p1.y) * (this.p3.x - this.p2.x) +
(this.p2.x * this.p2.x + this.p2.y * this.p2.y) * (this.p1.x - this.p3.x) +
(this.p3.x * this.p3.x + this.p3.y * this.p3.y) * (this.p2.x - this.p1.x)) / d;
const center = new Point(ux, uy);
const radius = Math.sqrt(
Math.pow(this.p1.x - center.x, 2) + Math.pow(this.p1.y - center.y, 2)
);
return { center, radius };
}
// 점이 외접원 내부에 있는지 확인
containsPoint(p) {
const { center, radius } = this.circumcircle();
const distance = Math.sqrt(
Math.pow(p.x - center.x, 2) + Math.pow(p.y - center.y, 2)
);
return distance < radius;
}
}
async function startDelaunay() {
initMap();
// 랜덤 점 생성 (방의 중심점)
const points = [];
const numPoints = 20; // 방의 개수
const roomSize = 2; // 방 크기
const margin = 2; // 방 사이의 최소 간격
// 방이 겹치는지 확인
function isOverlapping(x, y, size) {
for (let dy = -size - margin; dy <= size + margin; dy++) {
for (let dx = -size - margin; dx <= size + margin; dx++) {
const nx = x + dx;
const ny = y + dy;
if (nx >= 0 && nx < cols && ny >= 0 && ny < rows && map[ny][nx] === 0) {
return true;
}
}
}
return false;
}
// 안전한 위치 찾기
function findSafePosition() {
let x, y;
let attempts = 0;
const maxAttempts = 100;
do {
x = Math.floor(Math.random() * (cols - 2 * roomSize)) + roomSize;
y = Math.floor(Math.random() * (rows - 2 * roomSize)) + roomSize;
attempts++;
} while (isOverlapping(x, y, roomSize) && attempts < maxAttempts);
return attempts < maxAttempts ? {x, y} : null;
}
// 방 생성
for (let i = 0; i < numPoints; i++) {
const pos = findSafePosition();
if (!pos) continue; // 안전한 위치를 찾지 못하면 건너뛰기
points.push(new Point(pos.x, pos.y));
// 방 생성
for (let dy = -roomSize; dy <= roomSize; dy++) {
for (let dx = -roomSize; dx <= roomSize; dx++) {
const nx = pos.x + dx;
const ny = pos.y + dy;
if (nx >= 0 && nx < cols && ny >= 0 && ny < rows) {
map[ny][nx] = 0;
drawCell(nx, ny, 'white');
}
}
}
await sleep(50);
}
const triangles = delaunayTriangulation(points);
// 간선 추출
const edges = new Set();
for (const triangle of triangles) {
edges.add(new Edge(triangle.p1, triangle.p2));
edges.add(new Edge(triangle.p2, triangle.p3));
edges.add(new Edge(triangle.p3, triangle.p1));
}
const mstEdges = kruskalMST(Array.from(edges));
// MST 간선을 따라 통로 생성
for (const edge of mstEdges) {
await createCorridor(edge.p1, edge.p2);
}
generateEntrance();
}
// Delaunay Triangulation 알고리즘
function delaunayTriangulation(points) {
const triangles = [];
// 슈퍼 삼각형 생성 (모든 점을 포함하는 큰 삼각형)
// 초기 삼각형이 필요해 생성하며 나중에 제거함
const superTriangle = new Triangle(
new Point(-100, -100),
new Point(100, -100),
new Point(0, 100)
);
triangles.push(superTriangle);
for (const point of points) {
const badTriangles = [];
// 현재 점을 포함하는 삼각형 찾기
for (const triangle of triangles) {
if (triangle.containsPoint(point)) {
badTriangles.push(triangle);
}
}
// 나쁜 삼각형들의 간선 찾기
// 나쁜 삼각형은 너무 뾰족하거나 한 꼭지점에 너무 몰려 있는 못난 삼각형
const edges = new Set();
for (const triangle of badTriangles) {
edges.add(new Edge(triangle.p1, triangle.p2));
edges.add(new Edge(triangle.p2, triangle.p3));
edges.add(new Edge(triangle.p3, triangle.p1));
}
// 나쁜 삼각형 제거
for (const triangle of badTriangles) {
const index = triangles.indexOf(triangle);
if (index > -1) {
triangles.splice(index, 1);
}
}
// 새로운 삼각형 생성
for (const edge of edges) {
triangles.push(new Triangle(edge.p1, edge.p2, point));
}
}
// 슈퍼 삼각형과 관련된 삼각형 제거
return triangles.filter(triangle =>
!triangle.p1.equals(superTriangle.p1) &&
!triangle.p1.equals(superTriangle.p2) &&
!triangle.p1.equals(superTriangle.p3) &&
!triangle.p2.equals(superTriangle.p1) &&
!triangle.p2.equals(superTriangle.p2) &&
!triangle.p2.equals(superTriangle.p3) &&
!triangle.p3.equals(superTriangle.p1) &&
!triangle.p3.equals(superTriangle.p2) &&
!triangle.p3.equals(superTriangle.p3)
);
}
// Kruskal's MST 알고리즘
function kruskalMST(edges) {
// 간선을 가중치 순으로 정렬
edges.sort((a, b) => a.weight - b.weight);
const mst = [];
const sets = new Map();
// 각 점을 독립적인 집합으로 초기화
for (const edge of edges) {
if (!sets.has(edge.p1)) sets.set(edge.p1, new Set([edge.p1]));
if (!sets.has(edge.p2)) sets.set(edge.p2, new Set([edge.p2]));
}
// 사이클을 형성하지 않는 간선만 선택
for (const edge of edges) {
const set1 = sets.get(edge.p1);
const set2 = sets.get(edge.p2);
if (set1 !== set2) {
mst.push(edge);
// 두 집합 합치기
const union = new Set();
for (const p of set1) union.add(p);
for (const p of set2) union.add(p);
for (const point of union) {
sets.set(point, union); // 각 포인트가 새로운 union 집합을 참조하도록 갱신
}
}
}
return mst;
}
// 두 점 사이의 통로 생성
async function createCorridor(p1, p2) {
const dx = Math.sign(p2.x - p1.x);
const dy = Math.sign(p2.y - p1.y);
let x = p1.x;
let y = p1.y;
// x축 방향으로 먼저 이동
while (x !== p2.x) {
map[y][x] = 0;
drawCell(x, y, 'white');
x += dx;
await sleep(1);
}
// y축 방향으로 이동
while (y !== p2.y) {
map[y][x] = 0;
drawCell(x, y, 'white');
y += dy;
await sleep(1);
}
}
2. WFC 알고리즘
다소 난해했던 알고리즘
주변 셀에 따라 가능한 옵션을 줄이며 점차 결정하는 방식이다.
규칙을 설정해두는게 무엇보다 중요하다.
WFC는 Wave Function Collapse의 약자인데
Wave Function은 모든 타일이 겹쳐진 상태를 의미하고 Collapse는 결정하는 과정을 말한다.
다른 내용은 괜찮은데 엔트로피 개념이 갑자기 끼어들어서 헷갈렸다.
WFC에서의 엔트로피는 셀의 불확실성 정도, 그 셀에서 가능한 타일 후보 수를 의미한다.
가능한 타일이 많을수록 엔트로피가 높은 셀인 것.
흐름은 아래와 같다.
- 모든 셀은 타일 후보를 가지고 시작
- 가장 적은 옵션을 가진 셀 선택(엔트로피가 가장 낮은 셀)
- 그 셀이 가능한 타일 중 하나를 무작위로 결정(collapse)
- 전파(Propagation)
- 결정과 전파 반복
설정한 타일로 가득 채워진 맵을 얻을 수 있으며 타일을 잘 설정할수록 상당히 구조적인 맵이 나온다.
나는 불확실성으로 가득찬게 좋아서 타일을 8개 맘대로 집어넣었더니 결과물이 깔끔해 보이진 않는다.
개념을 확실히 정립하기 전에는 방 전체가 뚫린다던가 죄다 벽이라던가 구현이 어려웠다.
그래도 전파되며 만들어지는 모습이 아름답다.
// 2x2 타일 사전 정의
const tiles = [
{
name: "wall", // 전체 벽
data: [[1, 1], [1, 1]],
edges: { up: 1, right: 1, down: 1, left: 1 }
},
{
name: "floor", // 전체 통로
data: [[0, 0], [0, 0]],
edges: { up: 0, right: 0, down: 0, left: 0 }
},
{
name: "hall_h", // 수평 복도
data: [[1, 1], [0, 0]],
edges: { up: 1, right: 0, down: 1, left: 0 }
},
{
name: "hall_v", // 수직 복도
data: [[1, 0], [1, 0]],
edges: { up: 0, right: 1, down: 0, left: 1 }
},
{
name: "room_corner_top_left", // 위/왼쪽이 열린 방 구석
data: [[0, 0], [0, 1]],
edges: { up: 0, right: 0, down: 1, left: 0 }
},
{
name: "room_corner_bottom_right", // 아래/오른쪽 열린 방 구석
data: [[1, 0], [0, 0]],
edges: { up: 1, right: 0, down: 0, left: 0 }
},
{
name: "junction_T_up", // T자 모양 (위쪽 갈래)
data: [[0, 0], [1, 0]],
edges: { up: 0, right: 0, down: 1, left: 1 }
},
{
name: "dead_end_left", // 왼쪽에만 열린 막다른길
data: [[1, 1], [0, 1]],
edges: { up: 1, right: 1, down: 1, left: 0 }
}
];
// 붙으려는 상대방 타일의 방향을 찾기 위한 반대 방향 매핑
const opposite = {
up: "down",
down: "up",
left: "right",
right: "left"
};
// 타일 간 인접성 판단
function compatible(tileA, tileB, direction) {
return tileA.edges[direction] === tileB.edges[opposite[direction]];
}
// 셀 클래스 (1칸마다 타일 1개)
class WFC_TileCell {
constructor(x, y) {
this.x = x;
this.y = y;
this.options = tiles.slice(); // 가능한 타일들
this.collapsed = false;
}
collapse() {
const pick = this.options[Math.floor(Math.random() * this.options.length)];
this.options = [pick];
this.collapsed = true;
return pick;
}
getTile() {
return this.options[0];
}
}
async function startWFC() {
initMap();
const tileSize = 2; // 2x2 타일
const tileCols = Math.floor(cols / tileSize);
const tileRows = Math.floor(rows / tileSize);
const grid = Array.from({ length: tileRows }, (_, y) =>
Array.from({ length: tileCols }, (_, x) => new WFC_TileCell(x, y))
);
// collapse 루프
let pending = grid.flat().filter(cell => !cell.collapsed);
while (pending.length > 0) {
// 아직 collapse되지 않은 셀 중에서 가능한 옵션이 가장 적은 값 찾기
let minEntropy = pending.reduce((min, cell) => Math.min(min, cell.options.length), Infinity);
// 가능한 옵션 수가 최소인 셀들만 필터링
let choices = pending.filter(c => c.options.length === minEntropy);
// 그 중 하나를 랜덤 선택
let cell = choices[Math.floor(Math.random() * choices.length)];
const tile = cell.collapse();
// 타일을 실제 맵에 그리기
for (let dy = 0; dy < tileSize; dy++) {
for (let dx = 0; dx < tileSize; dx++) {
const mx = cell.x * tileSize + dx;
const my = cell.y * tileSize + dy;
if (mx < cols && my < rows) {
map[my][mx] = tile.data[dy][dx];
drawCell(mx, my, tile.data[dy][dx] === 1 ? 'black' : 'white');
}
}
await sleep(5);
// 주변 셀 옵션 줄이기
for (const [dir, [dx, dy]] of Object.entries({
up: [0, -1],
right: [1, 0],
down: [0, 1],
left: [-1, 0]
})) {
const nx = cell.x + dx;
const ny = cell.y + dy;
if (nx < 0 || ny < 0 || nx >= tileCols || ny >= tileRows) continue;
const neighbor = grid[ny][nx];
if (neighbor.collapsed) continue;
// 현재 셀과 호환되는 타일만 남김
neighbor.options = neighbor.options.filter(opt =>
compatible(tile, opt, dir)
);
}
pending = grid.flat().filter(c => !c.collapsed);
}
}
await generateEntrance();
}
완성
Delaunay Triangulation + MST
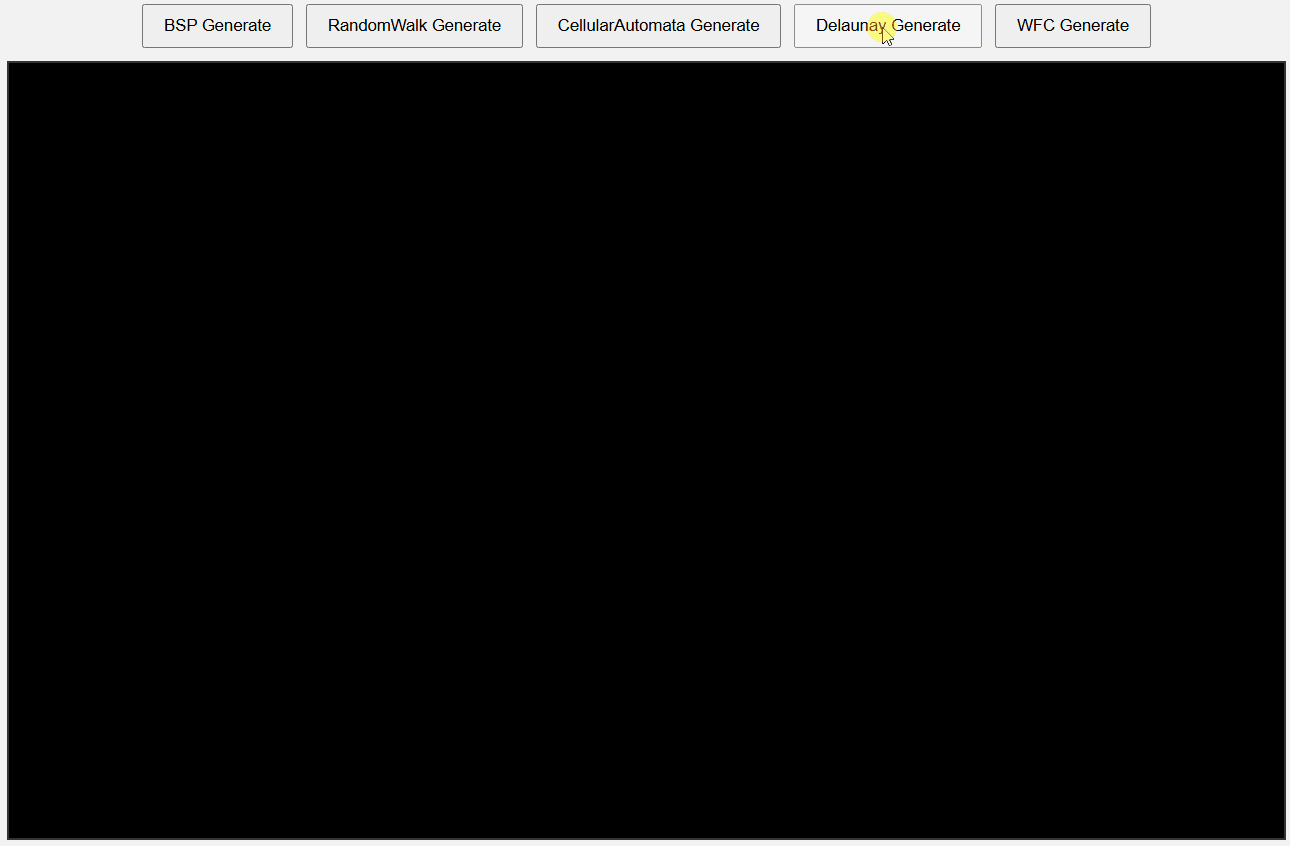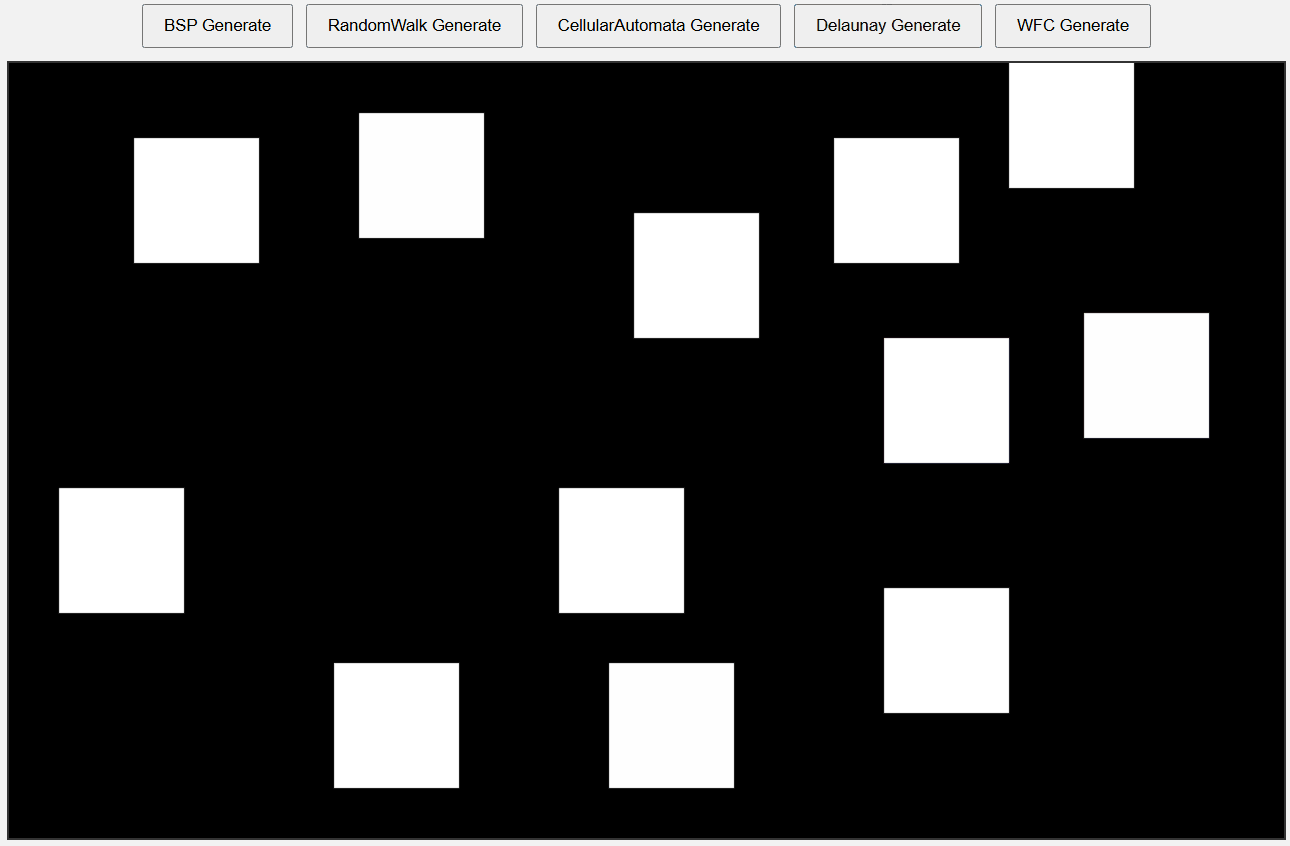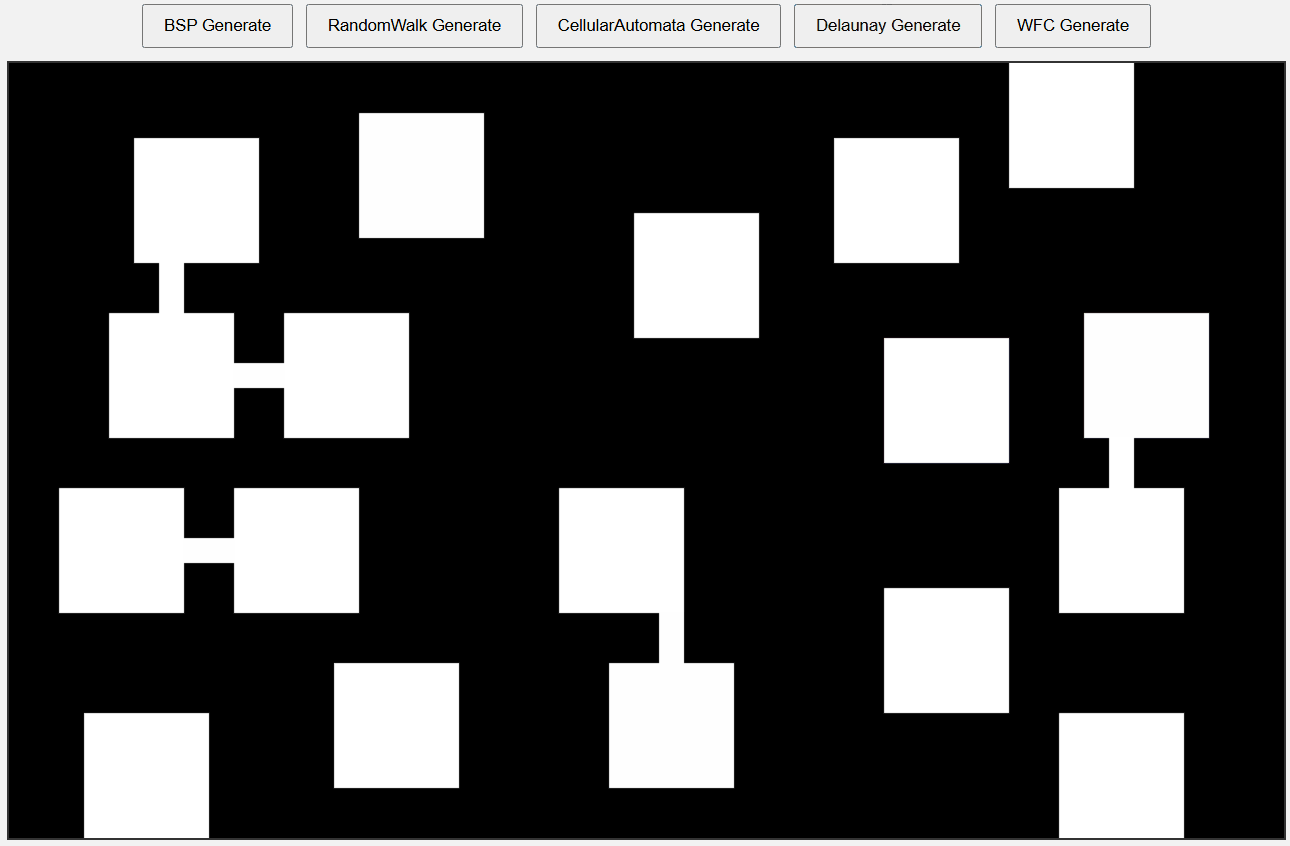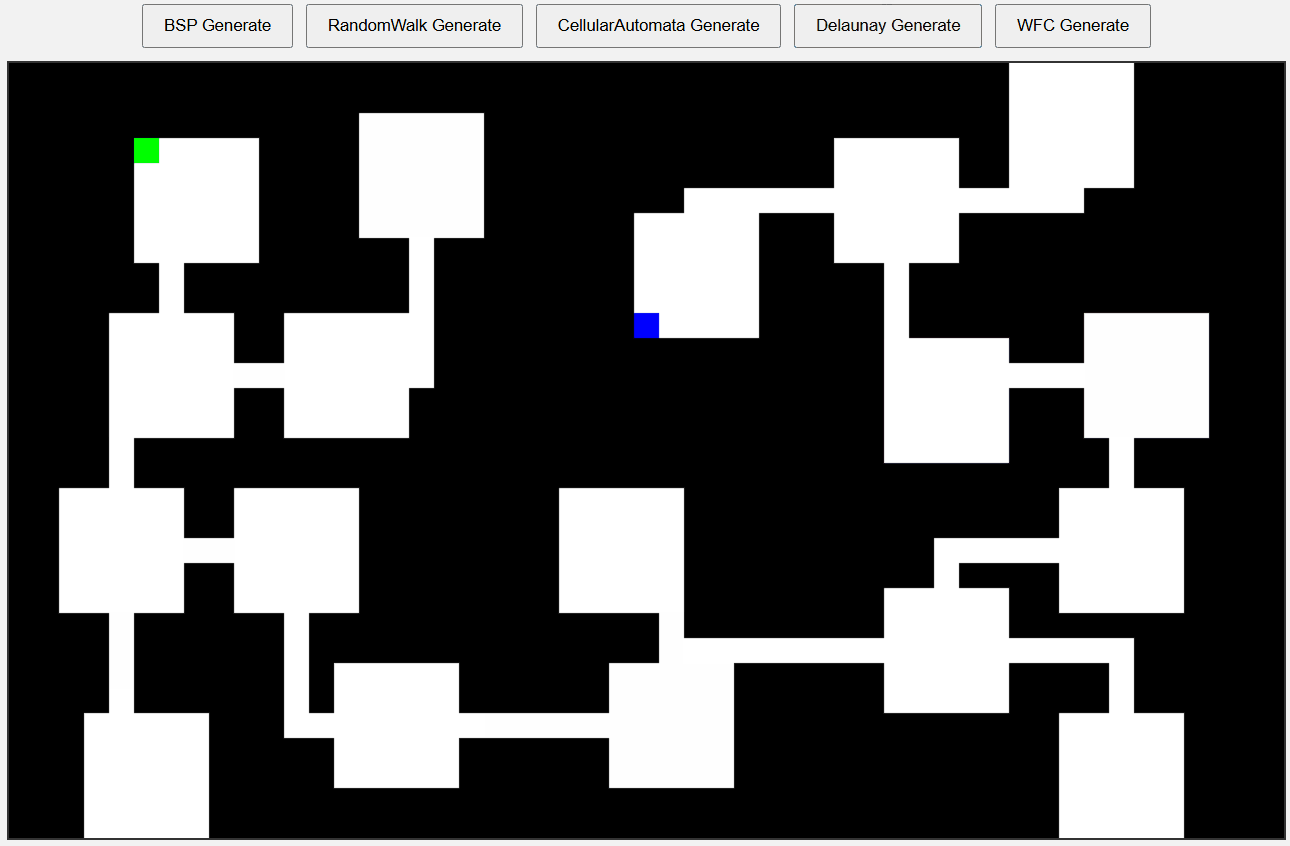
WFC
반성
동굴 지형같은 구불구불 무작위보다 구조적인 지형을 구성하는게 무엇보다 더 어려운 느낌이다.
우연하게 태어난 아름다움과 철저히 설계된 아름다움의 차이로 느껴진다.
아 감성적인 하루
코드 확인
Delaunay Triangulation + MST
Link to GitHub
WFC
Link to GitHub